代码实现LRU缓存机制

思路：要实现LRU缓存机制要保证：

O(1) 时间内完成如下操作：1.获取键 / 检查键是否存在2.设置键3.删除最先插入的键4.缓存满时，删除最近最久未用过的键

对于O(1)时间内完成检索键操作，很容易想到用Hash结构。这里我们可以用HashMap来存储数据。

对于条件4，我们需要找一个类似队列的结构来把最近最久未使用的和最近使用最多的键分别放到队列的两端，这样方便删、插。这里我们可以用LinkedList

具体过程如下：

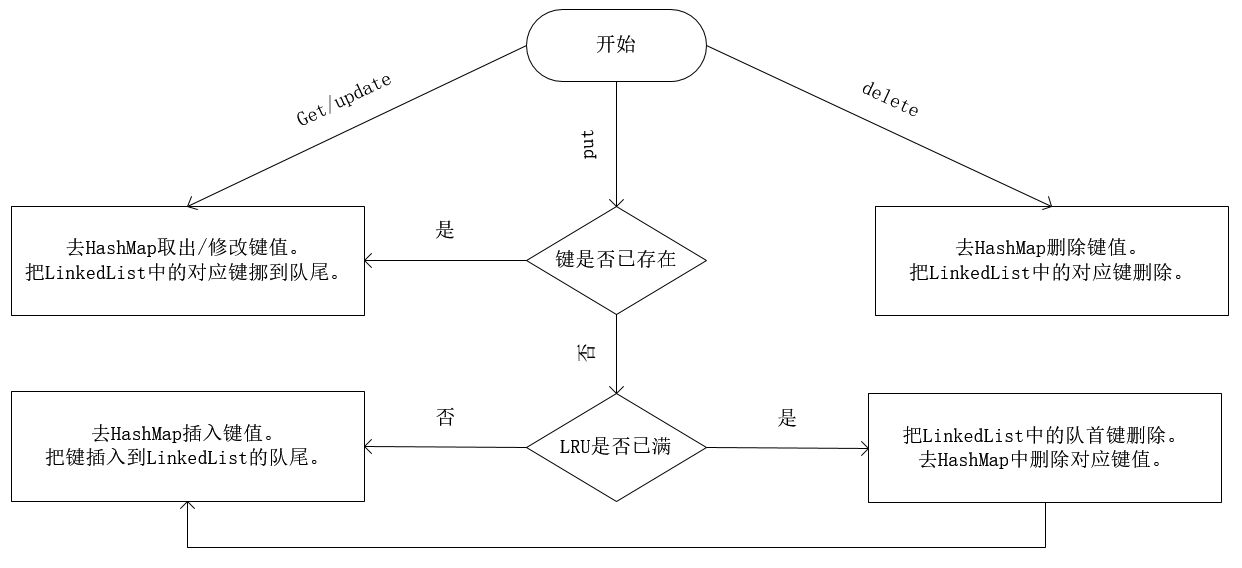
代码：

import java.util.HashMap;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;

public class LRUCache {
	List<Integer> qu=new LinkedList<Integer>();//存键，方便淘汰
	HashMap<Integer,Integer> map=new HashMap();//存数据
	int capacity;//LRU容量
    public LRUCache(int capacity) {//设置LRU容量
        this.capacity=capacity; 
    }
    
    public  int get(Integer key) {
    	if(!qu.isEmpty()&&!map.isEmpty()&&map.containsKey(key)){
    		qu.remove(key);
    		qu.add(key);//以上两步把键挪到队尾
    		return map.get(key);//返回对应键的值
    	}
        return -1;//对应键的值不存在
    }
    
    public  void put(Integer key, Integer value) {
    	if (map.containsKey(key)) {//键已存在，修改
    		qu.remove(key);
    		qu.add(key);//键挪到队尾
    		map.put(key, value);//放入新键值
		}else if(map.size()<capacity){//LRU未满，直接放入
        	qu.add(key);
        	map.put(key, value);
        }else{//LRU已满
        	int delkey=qu.remove(0);//淘汰最近最久未使用的键
        	map.remove(delkey);
        	qu.add(key);//插入新键值
        	map.put(key, value);
        }
    }

}

菜鸡吗，写代码难免会有不足。通过分析以上代码，我们发现，get和put（当键已存在时）操作的时间复杂度并不是O(1)而是O(n)，这是因为这两个操作要去linkedlist中删除对应的键，linkedlist删除键时会遍历和比较。

那么我们要做的就是把这个时间复杂度降到O(1)。

如果我们删除元素时，传入对应元素的指针，直接修改该元素前后元素的指针来删除这个元素，那么删除操作的时间复杂度就变成O(1)了。

为此我们需要自己写一个双向链表的结构，并提供O(1)时间复杂度下删除元素的操作方法。

class DLinkedNode {
    int key;
    int value;
    DLinkedNode prev;
    DLinkedNode next;
  }

  private void removeNode(DLinkedNode node){
    /**
     * Remove an existing node from the linked list.
     */
    DLinkedNode prev = node.prev;
    DLinkedNode next = node.next;

    prev.next = next;
    next.prev = prev;
  }

下面提供一种用Java已有API实现的一种傻瓜式写法：

class LRUCache extends LinkedHashMap<Integer, Integer>{
    private int capacity;
    
    public LRUCache(int capacity) {
        super(capacity, 0.75F, true);
        this.capacity = capacity;
    }

    public int get(int key) {
        return super.getOrDefault(key, -1);
    }

    public void put(int key, int value) {
        super.put(key, value);
    }

    @Override
    protected boolean removeEldestEntry(Map.Entry<Integer, Integer> eldest) {
        return size() > capacity; 
    }
}

/**
 * LRUCache 对象会以如下语句构造和调用:
 * LRUCache obj = new LRUCache(capacity);
 * int param_1 = obj.get(key);
 * obj.put(key,value);
 */